Advanced Machine Learning - Introduction to Deep Learning- Week2
This post is a summary for Advanced Machine Learning - Introduction to Deep Learning Course week2 in Coursera.
The simplest neural network: MLP
- Traingle problem
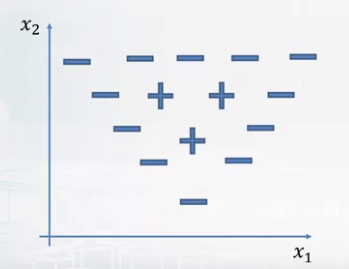
- Cannot solve the problem with linear model.
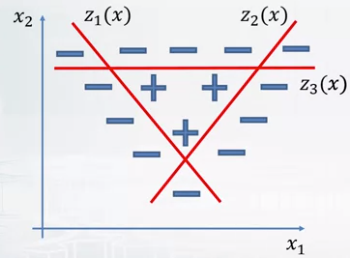
- Translate x1, x2 feature to 3 features z1, z2, z3
- Multi-layer Perceptron (MLP)
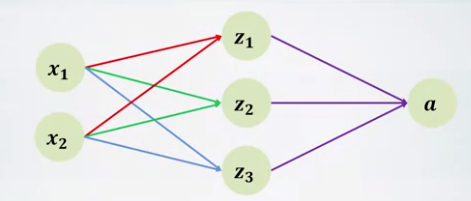
- Input layer containes features.
- Each node in hidden layer is a nueron.
- Apply activation function in hidden layer.
- Output layer predicts the result.
- Why we need a non-linear activation function
- Because algorithm turns in to a linear function without non-linear activation function.
- How to train MLP?
- how to train one nueron: SGD
- Do the same for the whole MLP
- Other problems:
- Many hidden layers -> need to caculate gradients automatically
- Many neurons -> need to calculate gradients fast.
- Chain rule
- \(z_1 = z_1(x_1, x_2)\).
- \(z_2 = z_2(x_1, x_2)\).
- \(p = p(z_1, z_2)\).
- \(z_1, z_2, p\) are differentiable
- \(\frac{\partial p} {\partial x_1} = \frac {\partial p} {\partial z_1} \frac {\partial z_1} {\partial x_1} + \frac {\partial p} {\partial z_2} \frac {\partial z_2} {\partial x_1}\).
- How this graph of derivatives helps
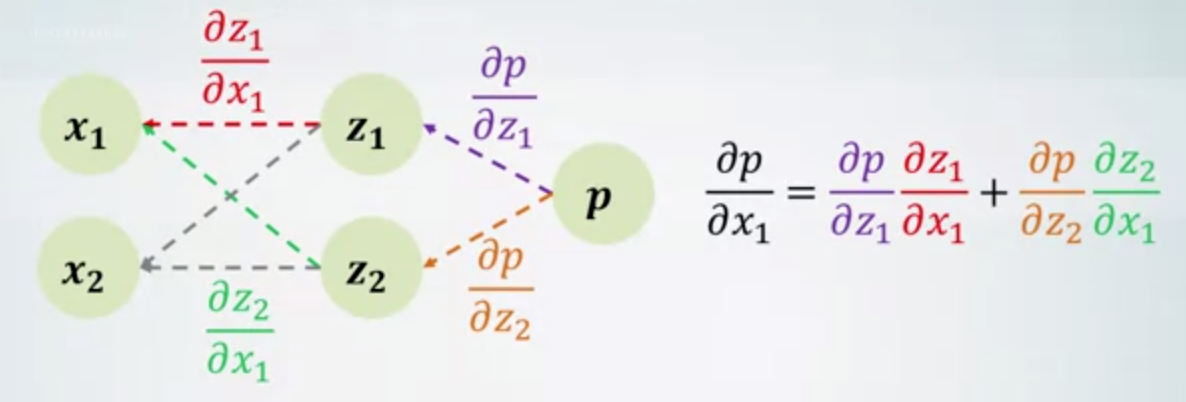
- How to calculate a derivative of node a w.r.t. node b:
- Find an unvisited path from a to b
- Multiply all edge values along this path
- Add to the resulting derivative
- loop above algorithm
- Summary
- We can use Chain rule to compute derivatives of composite functions
- We can use a computation graph of derivatives to compute them automatically
- How to apply a chain rule efficiently
- We can reuse previous computations.
- From the deepeset layer’s derivatvie, we can reuse it to upper layer.
- It’s called back-propagation.
- Back-propagation
- Forward pass
- We need to know at which points to take that derivative.
- take an input, produce an output
- Backward pass
- Made on graph of derivatives.
- need to take the input and incoming gradient
- Forward pass
Matrix derivatives
- Efficient MLP implementation
- using matrix for calculation
- forward pass for a dense layer is a matrix multiplication
- backward pass is a matrix multiplication as well.
- Jacobian
- The matrix of partial erivatives \(\frac {\partial h_i} {\partial x_j}\)
- \(J^h = \begin{bmatrix} \frac{\partial h_1} {\partial x_1} & \dots & \frac {\partial h_1} {\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial h_k} {\partial x_1} & \dots & \frac {\partial h_k} {\partial x_n} \end{bmatrix}\).
- Tensors
- Matrix by matrix derivative is a tensor
- Chain rule for tensors is not very useful
- Reading articles
- https://compsci697l.github.io/docs/vecDerivs.pdf
- https://www.math.uwaterloo.ca/~hwolkowi/matrixcookbook.pdf
TensorFlow framework
- What is TensorFlow?
- A tool to describe computational graphs
- A runtime for execution of these graphs
- input to operation will be a collection of tensors
- output will be a collection of tensors
- How the input looks like
- placeholder
- will be fed during graph execution
- x = tf.placeholder(tf.float32, (None, 10))
- variable
- Tensor with some value that is updated durign execution
- ex. weights matrix in MLP
- w = tf.get_variable(“W”, shape=(10, 20), dtype=tf.float32)
- Constant
- Tensor with a value that cannot be changed
- c = tf.constant(np.ones((4, 4)))
- placeholder
- Computational graph
- Tensorflow creates a defulat graph after importing
- Can get it with tf.get_default_graph()
- Can create graph with tf.Graph()
- Running a graph
- tf.Session encapsulates the environment in which tf.Operation objects are executed.
- You have to create a session and run graph
- Initialization of variables
- Can initalize with random uniformly value, etc.
- Have to initialize vefore running graph
- tf.global_variables_initializer()
- Trainalbe variables
- You can set trainable when back-propagation
- tf.get_variable(“x”, shape=(), dtype=tf.float32, trainable=False)
- Logging with tf.Print
- When you want to get synchronous value
- You can get it with TensorBoard
- Model Checkpoints
- Save variables state with tf.train.Saver
- These checkpoints only contain tensors and their values.
- So we have to define the graph exactly the same way.

Leave a comment